Visualizing Quantum Computing with FastHTMLVisualizing Quantum Computing with FastHTML

FastHTML

[FastHTML](https://fastht.ml) is a Python library for building web apps in pure Python. Under the hood it uses powerful lightweight frameworks like [Starlette](https://www.starlette.io) and [HTMX](https://htmx.org). I've already written about how [this website is built using FastHTML](/posts/fasthtml), so if you would like to learn more about FastHTML check out that blog post. In this post I'm going to focus on `__ft__` to create HTML representations of Python objects. Our use case will be to create representations of quantum gates and circuits for a quantum computing library I'm building called [skq](https://github.com/CarloLepelaars/skq). You don't have to know the details of quantum computing to appreciate the implementation of `__ft__`. This blog post is not an introduction to quantum computing. If you would like to understand the details of the representations given here you can check out the [free Quantum Computing for Programmers course I'm building called (q4p)](/q4p).

skq

[skq](https://github.com/CarloLepelaars/skq) is a [NumPy](https://numpy.org/)-based Python library for quantum computing. The goal is to make construction and analysis of quantum circuits as simple as possible. The circuits can then be converted to popular frameworks like [Qiskit](https://www.ibm.com/quantum/qiskit) or [OpenQASM](https://openqasm.com/) to run on real quantum computers. The skq library is used as an educational tool in [q4p](/q4p). Let's take a look at how we can display `skq` objects using `__ft__`.

__ft__ in Jupyter Notebooks

The `__ft__` method is a special method that allows us to render FastHTML objects in Jupyter Notebooks and FastHTML web apps. If you are using this functionality in Jupyter Notebooks make sure to first enable the rendering with `render_ft()`.

from fasthtml.jupyter import render_ft
render_ft()

Now all objects that have a `__ft__` implemented will be rendered in Jupyter.

Quantum Logic Gates

All `skq` [quantum logic gates](https://github.com/CarloLepelaars/q4p/blob/main/nbs/02-gates.ipynb) inherit from [QubitGate](https://carlolepelaars.github.io/skq/api/gates-qubit/#skq.gates.qubit.base.QubitGate), so patching `__ft__` to `QubitGate` will render all gates in the same way. For convenience we use [fastcore's](https://fastcore.fast.ai) `patch` decorator to add the `__ft__` method to `QubitGate`. I explain [how patch works in this blog post (3rd item)](/posts/fastcore-10). Let's create a FastHTML `Div` that visualizes the quantum gate and shows relevant properties styled with CSS. Don't worry about the details of this FastHTML code. The high-level context on the tags is as follows:

  • `Td` (Table Data) and `Tr` (Table Row) are HTML table elements to structure tables.
  • `Span` is a container that can be used to apply styling.
  • `H1`, `H2`, `H3` etc. create headers.
  • The `style` parameter accepts CSS properties to customize the appearance of any FastHTML element
# FastHTML tags
from fasthtml.common import *
# Patch methods on a class
from fastcore.all import patch
# Base class for skq quantum logic gates
from skq.gates.qubit import QubitGate

@patch
def __ft__(self: QubitGate):
    # CSS to style the visualizations
    code_style = "font-family: monospace; white-space: pre; font-size: 14px; padding: 12px; background: #000000; color: #00ff00; border: 2px solid #0088ff; border-radius: 4px; width: fit-content;"
    # Table containing properties about the quantum logic gate
    props_table = Table(
    Tr(Td("Number of Qubits:"), Td(str(self.num_qubits))),
    Tr(
        Td("Is Pauli:"), 
        Td(Span(str(self.is_pauli()), style=f"color: {'#00ff00' if self.is_pauli() else '#ff0000'}"))
    ),
    Tr(
        Td("Is Clifford:"), 
        Td(Span(str(self.is_clifford()), style=f"color: {'#00ff00' if self.is_clifford() else '#ff0000'}"))
    ), 
    Tr(
        Td("Is Hermitian:"), 
        Td(Span(str(self.is_hermitian()), style=f"color: {'#00ff00' if self.is_hermitian() else '#ff0000'}"))
    ),
    style="color: #e0e0e0"
)
    return Div(
        # Name of the quantum logic gate
        H1(self.__class__.__name__, style="color: #00ff00; text-align: center; margin-bottom: 20px;"),
        # Representations
        Div(
            Div(H3("Diagram", style="margin-bottom: 10px;"), P(self.draw(), style=code_style), style="flex: 1; padding: 0 10px;"),
            Div(H3("Matrix", style="margin-bottom: 10px;"), P(str(self.__array__().round(3)), style=code_style), style="flex: 1; padding: 0 10px;"),
            *([Div(H3("OpenQASM", style="margin-bottom: 10px;"), P(self.to_qasm(qubits=[i for i in range(self.num_qubits)]), style=code_style), style="flex: 1; padding: 0 10px;")]),
            style="display: flex; flex-wrap: wrap; gap: 15px; margin-bottom: 25px;"
        ),
        # Table of properties
        Div(
            Div(H3("Properties", style="color: #ffffff; margin-bottom: 10px;"), props_table, style="flex: 1; padding: 0 10px;"),
            style="display: flex; flex-wrap: wrap; gap: 15px;"
        ),
        # Global CSS styling
        style="background: #000000; color: #e0e0e0; padding: 20px; border-radius: 8px;"
    )

Now every `QubitGate` object in `skq` will be rendered when `__ft__` is called. Let's check out how this looks for one of the simplest gates in quantum computing called the `X` (NOT) gate.

from skq.gates.qubit import X
X().__ft__()

X

Diagram

┌───┐ q: ┤ X ├ └───┘

Matrix

[[0.+0.j 1.+0.j] [1.+0.j 0.+0.j]]

OpenQASM

x q[0];

Properties

Number of Qubits: 1
Is Pauli: True
Is Clifford: True
Is Hermitian: True

Or for example take a [multi-qubit gate](https://github.com/CarloLepelaars/q4p/blob/main/nbs/03-multi.ipynb) like the `CH` (Controlled-Hadamard) gate:

from skq.gates.qubit import CH
CH().__ft__()

CH

Diagram

q_0: ──■── ┌─┴─┐ q_1: ┤ H ├ └───┘

Matrix

[[ 1. +0.j 0. +0.j 0. +0.j 0. +0.j] [ 0. +0.j 1. +0.j 0. +0.j 0. +0.j] [ 0. +0.j 0. +0.j 0.707+0.j 0.707+0.j] [ 0. +0.j 0. +0.j 0.707+0.j -0.707+0.j]]

OpenQASM

ch q[0], q[1];

Properties

Number of Qubits: 2
Is Pauli: False
Is Clifford: True
Is Hermitian: True

Quantum Circuits

We can also use this functionality to visualize quantum algorithms. In `skq` quantum algorithms are represented as `Circuit` objects. `Circuit` has a `draw` method that uses [Qiskit](https://www.ibm.com/quantum/qiskit)'s visualization functionality under the hood. We can use FastHTML to create our own styling.

from fasthtml.common import *
from fastcore.all import patch
from skq.circuits import Circuit

@patch
def __ft__(self: Circuit):
    # Custom CSS styling
    style = '''font-family: monospace; white-space: pre; font-size: 14px;
                padding: 12px; background: #000000; color: #00ff00;
                border: 2px solid #0088ff; border-radius: 4px;
                width: fit-content;'''
    return Div(
        # Circuit name
        H1(self.__class__.__name__, style=style),
        # Circuit diagram
        P(self.draw(), style=style),
    )

Now every `Circuit` in `skq` will have our styling. One of the most iconic quantum algorithms is [Grover's search algorithm](https://github.com/CarloLepelaars/q4p/blob/main/nbs/05-grover.ipynb). This algorithm is available out of the box in `skq`. Let's have a look at a simple layout of the algorithm:

import numpy as np
from skq.circuits import Grover

# Grover's algorithm as a Circuit object
grover = Grover().circuit(n_qubits=3, 
                 target_state=np.array([0, 0, 0, 0, 1, 0, 0, 0]), 
                 n_iterations=1)
grover.__ft__()

Circuit

┌───┐┌──────────────┐┌──────────────────┐┌─┐ q_0: ┤ H ├┤0 ├┤0 ├┤M├────── ├───┤│ ││ │└╥┘┌─┐ q_1: ┤ H ├┤1 PhaseOracle ├┤1 GroverDiffusion ├─╫─┤M├─── ├───┤│ ││ │ ║ └╥┘┌─┐ q_2: ┤ H ├┤2 ├┤2 ├─╫──╫─┤M├ └───┘└──────────────┘└──────────────────┘ ║ ║ └╥┘ c: 3/══════════════════════════════════════════╩══╩══╩═ 0 1 2


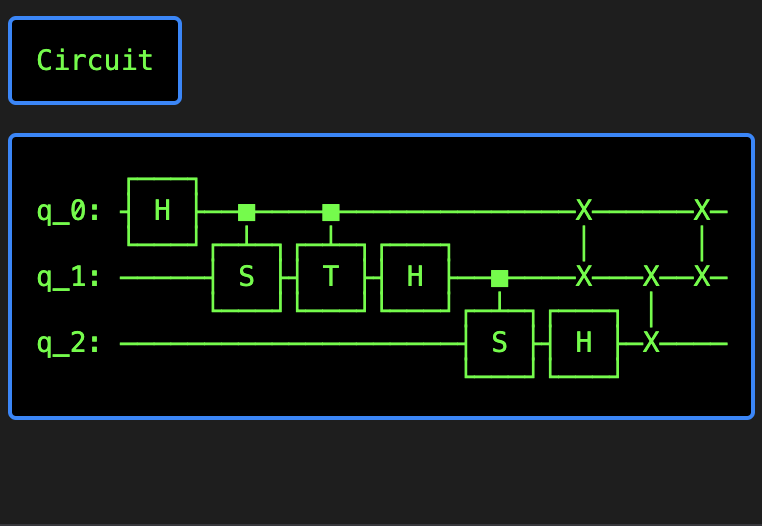
For fun let's also look at a custom `skq` Circuit. This is a `Circuit` that represents a [Quantum Fourier Transform (QFT)](https://en.wikipedia.org/wiki/Quantum_Fourier_transform).

from skq.gates.qubit import H, I, CS, CT, SWAP
from skq.circuits import Circuit, Concat
                 
qft_3 = Circuit(
    [
        Concat([H(), I(), I()]),
        Concat([CS(), I()]),
        Concat([CT(), I()]),
        Concat([I(), H(), I()]),
        Concat([I(), CS()]),
        Concat([I(), I(), H()]),
        Concat([SWAP(), I()]),
        Concat([I(), SWAP()]),
        Concat([SWAP(), I()]),
    ]
)
qft_3.__ft__()

Circuit

┌───┐ q_0: ┤ H ├──■────■──────────────X──────X─ └───┘┌─┴─┐┌─┴─┐┌───┐ │ │ q_1: ─────┤ S ├┤ T ├┤ H ├──■────X───X──X─ └───┘└───┘└───┘┌─┴─┐┌───┐ │ q_2: ────────────────────┤ S ├┤ H ├─X──── └───┘└───┘


I hope this gives you a good idea on how you can use `__ft__` to create your own representations of Python objects. This blog post is an experiment on how to create the best representations for the [skq](https://github.com/CarloLepelaars/skq) library. The goal is to create intuitive representations to serve as an educational tool for quantum computing in the [q4p](/q4p) course. Feedback on the project is always welcome!

Conclusion

FastHTML has the potential to change how we represent Python objects, especially in Jupyter Notebooks and FastHTML web apps. As a practical use case we have seen how HTML representations can make it easier to interpret quantum gates and algorithms. I hope you have learned something new and you now have sufficient context to integrate FastHTML rendering into your own projects.

q4p

If you are interested in learning more about quantum computing, I've been working on a free open source project for quantum computing education. It's called [q4p](/q4p). It aims to demystify quantum computing using Python and focuses on applications. All [q4p](/q4p) lessons are available on [Github](https://github.com/CarloLepelaars/q4p) and [Kaggle](https://www.kaggle.com/carlolepelaars/code?query=q4p+-). There is also a [curated resources page](https://github.com/CarloLepelaars/q4p/blob/main/resources.md) where you will find links to books, websites, courses, videos, blog posts, code repositories and podcasts.
Back to Posts Overview
© Carlo Lepelaars 2024 - 𝕏