Introduction
So I was reading ["The Motor Racing Book" by Suellio Almeida](https://amzn.to/4fRRlua), which is a great practical guide on how to race cars on different tracks. In the introduction, Suellio goes into avoiding bad habits and how to gradually integrate new techniques. He mentions the Ebbinghaus Forgetting Curve to stress the importance of repeating information. Re-reading the same information at different times helps you retain and take in information from different perspectives. Let's see what we can learn from Ebbinghaus' work on learning.
Ebbinghaus
At the end of the 19th century, German psychologist Hermann Ebbinghaus set out to measure his own memory retention by trying to remember nonsense syllables. His [forgetting curve](https://en.wikipedia.org/wiki/Forgetting_curve) models his own memorization capability when there is no attempt to retain it. Ebbinghaus modelled his own rate of forgetting as:
$$
b = \frac{100k}{log^{c}(t) + k}
$$
where $b$ indicates retention rate, $t$ indicates time in minutes, $k=1.84$ and $c=1.25$. For example, a 10% retention rate means that relearning all missed items required 90% of the time of the 1st learning session. This is a fitted logistic function with fitted parameters $k$ and $c$. Simplifying this expression numerically:
$$
b = \frac{184}{log^{1.25}(t) + 1.84}
$$
The retention curve looks like this:
One would expect that the retention curve will be less steep after subsequent learning sessions. Indeed, other researchers have modelled the effect of repetition with an exponential decay.
Stability of Memory
[Piotr Wozniak et al. (1995)](https://web.archive.org/web/20100920055038/http://ane.pl/pdf/5535.pdf) worked on long-term memory stability and proposed a simple exponential model for information retrievability:
$$
R = e^{-\frac{t}{S}}
$$
where $R$ is the retrievability of information, $t$ is time in days and $S$ is the stability of memory.
The higher the stability of memory, the better information is retained over time. As seen in the plot below, you can see that with low stability information can be completely forgotten in less than a week. I think we can all relate to a scenario where this happened for us. Perhaps from studying intensely the night before an exam and then never revisiting the material again. The stability increases by repeating and studying the information deeply. Wozniak et al. go deeper into how $S$ improves with spaced repetition in [their paper](https://web.archive.org/web/20100920055038/http://ane.pl/pdf/5535.pdf).
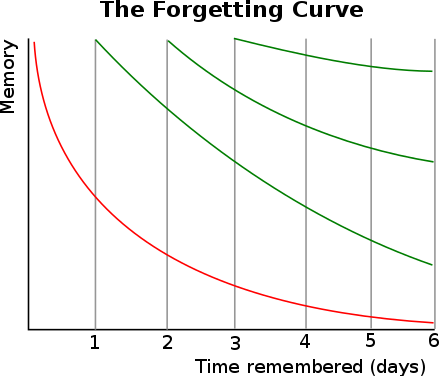 Ebbinghaus Forgetting Curve
Ebbinghaus Forgetting Curve 